Wave and sound

Transverse waves

• Particle moves up and down, perpendicular to the motion of the wave
• Crest: $y = A$ and trough: $y = -A$

$$\begin{align*} k &= \frac{2\pi}{\lambda} \\ v &= f\lambda = \frac{\omega}{k} \\ f &= \frac{\omega}{2\pi} \\ T &= \frac{1}{f} \end{align*}$$

• $k$: wave number (m$^{-1}$)

info

Wave speed on a string: $v = \large\sqrt{\frac{T}{\mu}}$

• $T$: equilibrium tension of the string
• $\mu$: mass per unit length of the string

Challenging question

A uniform rope of mass $m$ and length $L$ hangs vertically from a ceiling. The time $t$ it takes for a transverse wave to travel the length of the rope is:

$$\begin{align*} T = \mu gy &\text{ and } \mu = \frac{m}{L} \\ t = \frac{y}{v} &= \int_0^L \frac{dy}{v} \\ &= \int_0^L \sqrt{\frac{\mu}{\mu gy}} dy \\ &= \frac{1}{\sqrt{g}} \int_0^L \frac{dy}{\sqrt{y}} \\ &= 2\sqrt{\frac{L}{g}} \end{align*}$$

Wave equation for transverse waves

Wave traveling +ve x-direction:

$$y(x,t) = A\cos(kx-\omega t)$$

Wave traveling −ve x-direction:

$$y(x,t) = A\cos(kx+\omega t)$$

Superposition

If $y_1$ and $y_2$ are incoming wave and reflected wave, their resultant wave $y = y_1 + y_2$

$$\begin{align*} v_y(x,t) &= \omega A\sin(kx-\omega t) \\ v_{max} &= \omega A \\ a_y(x,t) &= -\omega^2 A\cos(kx-\omega t) \\ a_{max} &= \omega^2 A \end{align*}$$

warning

$v_y$ is the speed of a particle, not the wave speed.

Energy in wave motion

• $P$: power of the wave
• $I$: intensity of the wave (W/m$^2$)

$$\begin{align*} P(x,t) &= \sqrt{\mu T}\omega^2A^2sin^2(kx-\omega t) \\ P_{max} &= \sqrt{\mu T}\omega^2A^2 \\ P_{av} &= \frac{1}{2}P_{max} \\ I &= \frac{P}{4\pi r^2} \end{align*}$$

Reflection of transverse waves

Fixed boundary	Open boundary

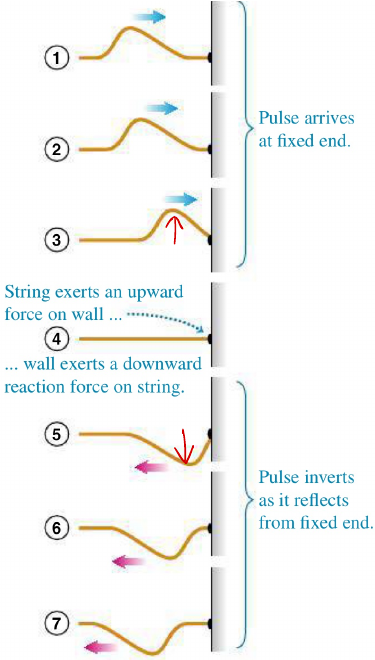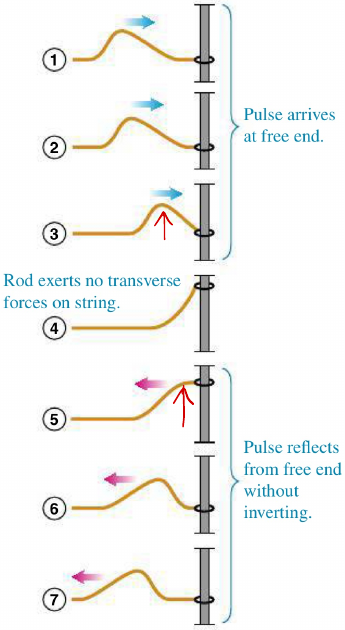Standing waves

• Node: zero amplitude, destructive interference
• Antinode: maximum amplitude, constructive interference

Standing waves for fixed boundary condition

$$\begin{align*} y(x,t) &= 2A\sin(kx)\sin(\omega t) \end{align*}$$

• Nodes at $x = 0,\large\frac{\lambda}{2}\normalsize,\lambda,\large\frac{3\lambda}{2}\normalsize,...$
• Antinodes at $x = \large\frac{\lambda}{4}\normalsize,\large\frac{3\lambda}{4}\normalsize,\large\frac{5\lambda}{4}\normalsize,...$

Standing waves for open boundary condition

$$\begin{align*} y(x,t) &= 2A\cos(kx)\cos(\omega t) \end{align*}$$

• Nodes at $x = \large\frac{\lambda}{4}\normalsize,\large\frac{3\lambda}{4}\normalsize,\large\frac{5\lambda}{4}\normalsize,...$
• Antinodes at $x = 0,\large\frac{\lambda}{2}\normalsize,\lambda,\large\frac{3\lambda}{2}\normalsize,...$

Harmonics

Fundamental frequency ($n = 1$):

$$f_1 = \frac{v}{2L}$$

Second harmonic ($n = 2$):

$$f_2 = 2f_1$$

n-th harmonic:

$$f_n = nf_1$$

• Length of the string $L = \frac{n\lambda}{2}$

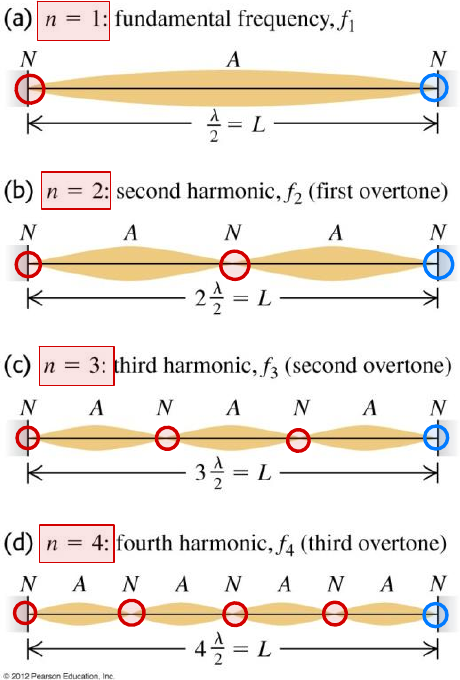
Sound waves

Beats

Superposition of two sound waves

$$\begin{align*} f_{beat} &= |f_1-f_2| \\ T_{beat} &= \frac{1}{|f_1-f_2|} \end{align*}$$

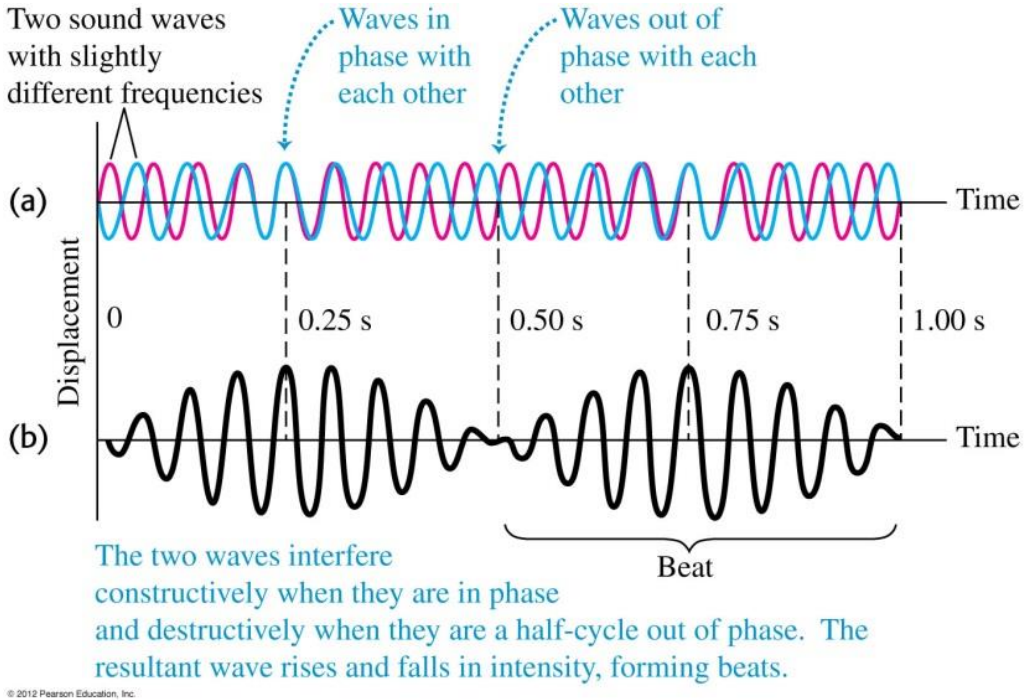
Doppler effect of sound

$$\begin{align*} f_L = \left(\frac{v+v_L}{v+v_S}\right)f_S \end{align*}$$

• $f_L$: frequency at the listener
• $f_S$: frequency of the source
• $v_L$: velocity of the listener
• $v_S$: velocity of the source

warning

For $v_L$ and $v_S$: direction pointing from listener to source is positive

e.g. If the listener is approaching the source, while the source is approaching the listener:

$v_L > 0 \text{ and } v_S < 0 \Rightarrow f_L > f_S$

Doppler effect of light (out of syllabus?)

$$\begin{align*} f_R = \sqrt{\frac{c-v}{c+v}}f_S \end{align*}$$

where $v$ is the relative velocity between the receiver and the source