Periodic motion
Simple harmonic motion (SHM)
- : angular frequency (rad/s)
- : frequency (Hz)
General solution
Phase angle
If
If
It tells the displacement of the particle at
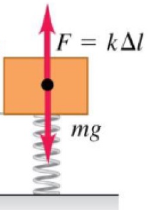
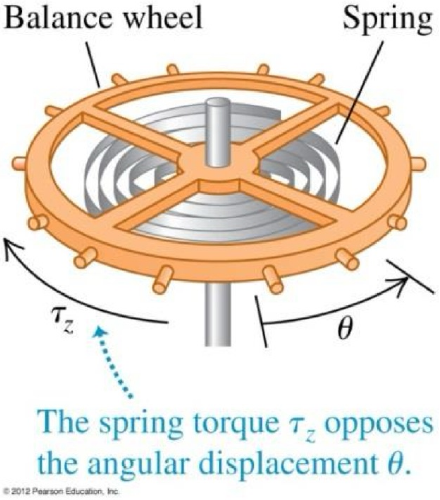
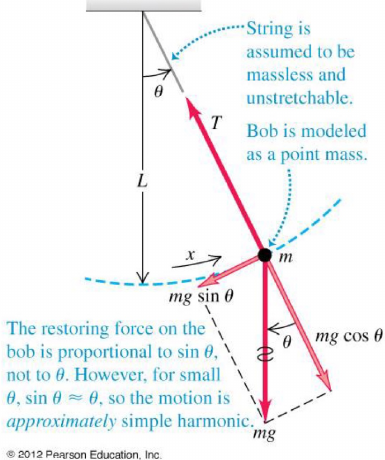
Simple harmonic oscillators
| Block-spring | Angular oscillator | Simple pendulum | Physical pendulum |
|---|---|---|---|
| : spring constant | : torsion constant | : length of the pendulum | : distance from the pivot to its CG |
 |  |  | 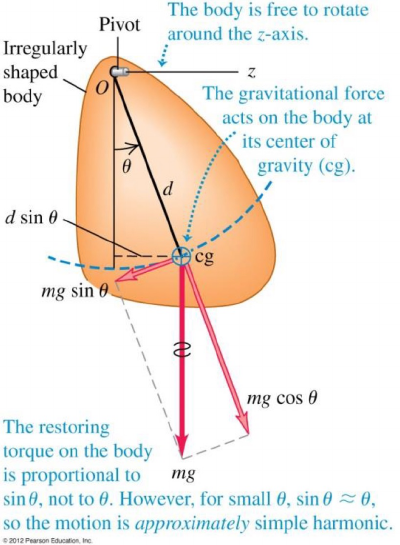 |
Conservation of energy in SHM
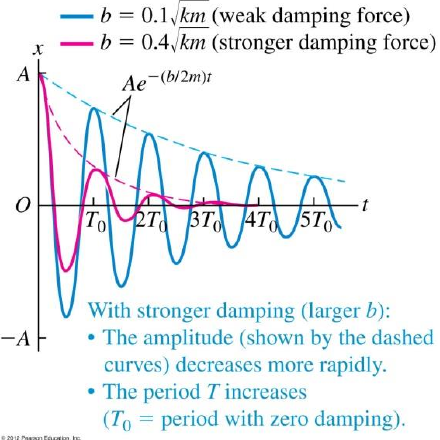
Damped harmonic oscillator
- : damping constant
- : damped angular frequency
info
- : under damping (oscillation dies off)
- : critical damping (no oscillation, return to equilibrium in shortest time)
- : over damping (no oscillation)
Forced harmonic oscillation
- : driving angular frequency
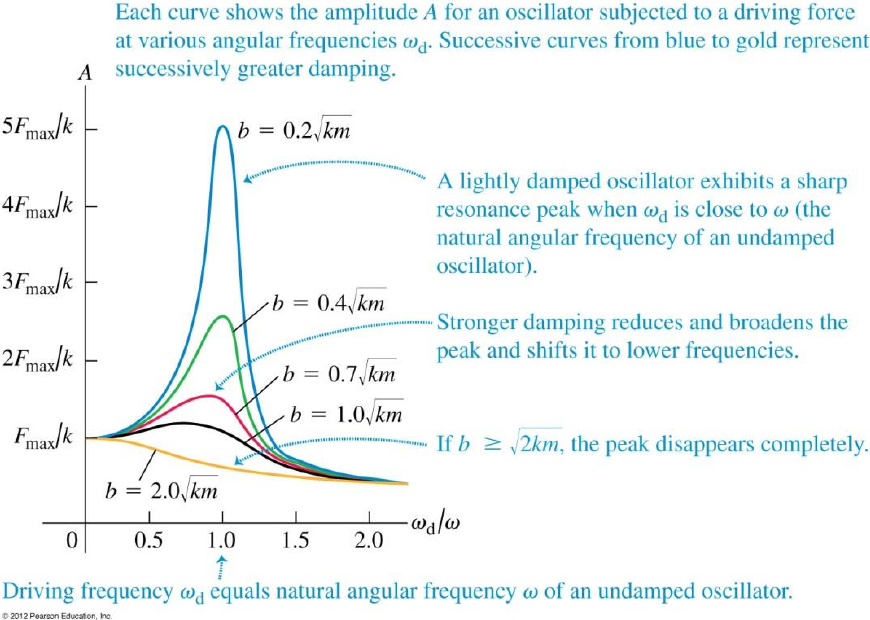
Resonance
- When (natural angular frequency of an undamped oscillator), reaches maximum (resonance peak)
- Smaller (lighter damping) gives a sharper peak
- If , the peak disappears completely