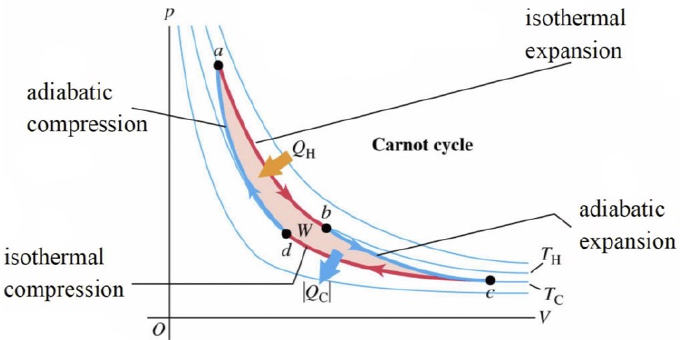
Thermodynamics

Basic info (click to expand)

Number of moles $n = \frac{m}{M} = \frac{N}{N_A}$

• $M$: molar mass (kg/mol), mass of 1 mole of the substance
• $N$: number of molecules
• $N_A = 6.02\times10^{23}$ mol$^{-1}$ : Avogadro constant

Pressure $= \frac{\text{Force}}{\text{Area}}$

Density $= \frac{\text{Mass}}{\text{Volume}}$

Litter to cubic meter: $1$L = $1\times10^{-3}$ m$^3$

Summary

First law of thermodynamics: $\Delta U = Q_{in} - W_{by}$

	Change in internal energy	Heat	Work done
	$U = \frac{f}{2}nRT$	$Q_{in} = nC\Delta T$	$W_{by} = \int_{V_1}^{V_2} pdV$
Isothermal ($\Delta T = 0$)	$\Delta U = 0$	$Q_{in} = W_{by}$	$W_{by} = nRT\ln\left(\frac{V_2}{V_1}\right)$
Isochoric ($\Delta V = 0$)	$\Delta U = Q_{in} = \frac{f}{2}nR\Delta T$	$Q_{in} = nC_V\Delta T$	$W_{by} = 0$
Isobaric ($\Delta p = 0$)	$\Delta U = \frac{f}{2}p\Delta V = \frac{f}{2}nR\Delta T$	$Q_{in} = nC_p\Delta T$	$W_{by} = p\Delta V = nR\Delta T$
Adiabatic ($Q_{in} = 0$)	$\Delta U = -W_{by}$	$Q_{in} = 0$	$W_{by} = \frac{1}{\gamma-1}(p_1V_1 - p_2V_2)$

Ideal gas law

$$\begin{align*} pV = nRT = NkT \end{align*}$$

• $R = 8.314$ J/mol$\cdot$K : universal gas constant
• $k = 1.381\times10^{-23}$ J/K : Boltzmann constant

First law of thermodynamics

$$\Delta U = Q_{in} - W_{by}$$

• $\Delta U$: change in internal energy
• path-independent
• For a cyclic process, $\Delta U = 0$

• $Q_{in}$: heat enters into system from surroundings
• path-dependent

• $W_{by}$: work done by the system
• = Area under p-V curve
• path-dependent
• Expansion: $W_{by} > 0$
• Compression: $W_{by} < 0$

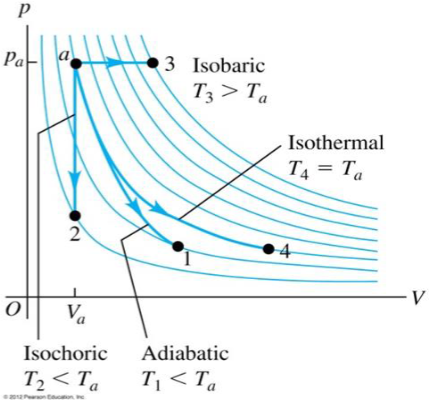
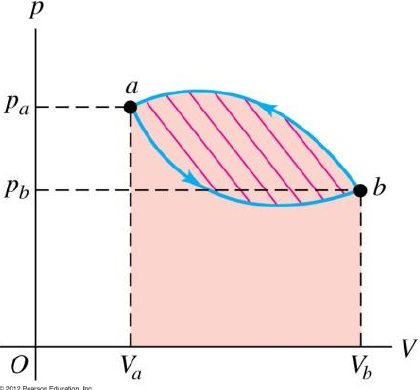
Example cyclic process with $W_{net} < 0$

KE of ideal gas

Total translational KE of all molecules:

$$K_{tot} = \frac{3}{2}nRT = \frac{3}{2}NkT$$

Root-mean-square speed of molecules:

$$v_{rms} = \sqrt{\frac{3RT}{M}} = \sqrt{\frac{3kT}{m}}$$

Most probable speed of molecules:

$$v_{mp} = \sqrt{\frac{2RT}{M}} = \sqrt{\frac{2kT}{m}}$$

Average speed of molecules:

$$v_{av} = \sqrt{\frac{8RT}{\pi M}} = \sqrt{\frac{8kT}{\pi m}}$$

Molar heat capacity of ideal gas

At constant volume:

$$C_V = \frac{f}{2}R$$

At constant pressure:

$$C_p = \frac{f+2}{2}R$$

Adiabatic index:

$$\gamma = \frac{C_p}{C_V} = \frac{f+2}{f}$$

Degrees of freedom $f$

Monoatomic gas:

• $f = 3$ and $\gamma = \frac{5}{3}$
• Translation only

Diatomic gas:

• $f = 5$ and $\gamma = \frac{7}{5}$
• Translation + rotation
• At very high temperature:
  • $f = 7$ and $\gamma = \frac{9}{7}$
  • Translation + rotation + vibration

Adiabatic process

• $Q = 0$ : no heat enters into or exits from the system
• e.g. free expansion of gas

$$\begin{align*} pV^\gamma &= \text{constant} \\ TV^{\gamma-1} &= \text{constant} \\ W_{by} &= \frac{1}{\gamma-1}(p_1V_1 - p_2V_2) \end{align*}$$

Second law of thermodynamics

Carnot cycle

Carnot engine

Thermal efficiency:

$$\begin{align*} e &= \frac{W}{|Q_H|} = 1 - \frac{|Q_C|}{|Q_H|} \\ e &\le 1 - \frac{T_C}{T_H} < 1 \end{align*}$$

where $T_C$ and $T_H$ are in Kelvin

Refrigerator

Coefficient of performance:

$$\begin{align*} K &= \frac{|Q_C|}{|W|} = \frac{|Q_C|}{|Q_H| - |Q_C|} \\ K &\le \frac{T_C}{T_H - T_C} \end{align*}$$

where $T_C$ and $T_H$ are in Kelvin