Radial acceleration:
arad=rv2
Period:
T=v2πr=2πaradr
nv=rmv2−mg>rgif n>0
- n: normal force (at the top of the cylinder) acting on the object
- if n≤0 (i.e. v≤rg) then the object loses contact with the surface
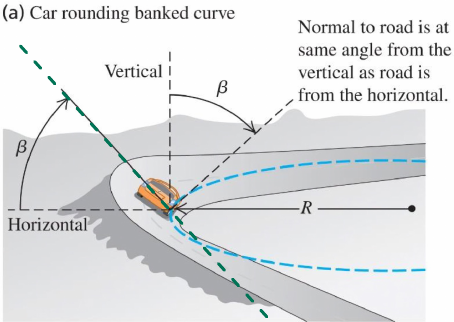
aradT=gtanθ=2πgLcosθ ∑Fx∑Fy∴vmax=rmv2=nsinθ+μsncosθ=0=ncosθ−μsnsinθ−mg=gr1−μstanθtanθ+μs≥(vflat)max(1)(2)