Basic info (click to expand)
- s=rθ , ω=dtdθ , α=dtdω
- Anticlockwise rotation: Δθ>0
- Direction of ω is defined by the right-hand thumb rule
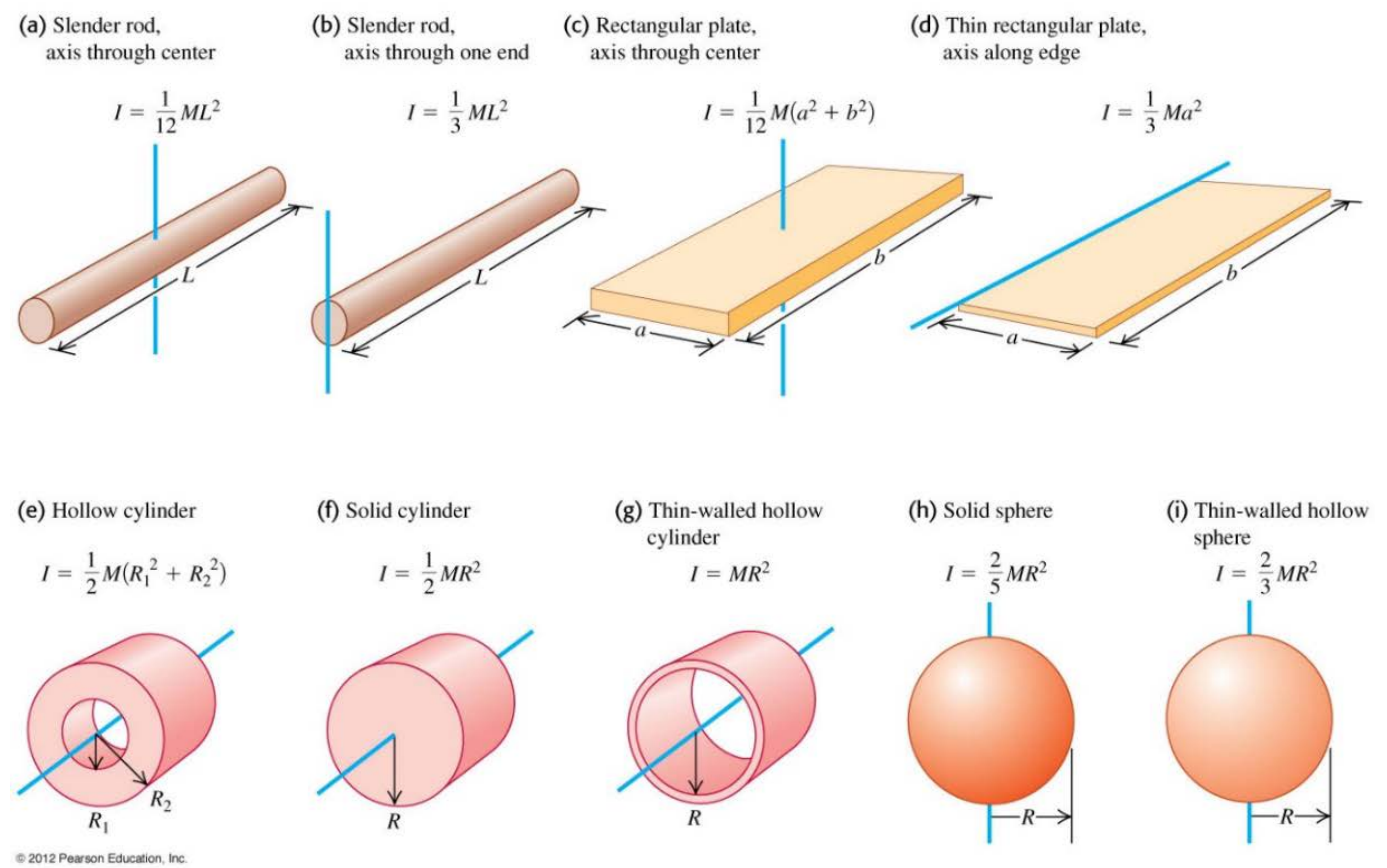
vtanatanarad=rω=rα=rv2=ω2rSI unit: kg⋅m2
IKrot=i∑miri2=∫r2dm=∫r2ρdr=21Iω2
- ρ=LM (density of the rod)
- Ip: I about an axis parallel to the axis through its center of mass
- Icm: I about an axis through its center of mass
- M: total mass of the rigid body
- d: perpendicular distance between the two axises
Ip=Icm+Md2
SI unit: N⋅m
ττWP=dtdL=r×F=rFsinθ=Iα=∫τdθ=τω
- θ: angle (anticlockwise) from the radial arm to the line of action
- Direction of τ is defined by the right-hand thumb rule
- vcm=rω
- Contact point must be at rest: v=0
- There must be static friction which is always up the slope, but it does no work
