Work and kinetic energy

Kinetic energy

Translational:

$$K_{tr} = \frac{1}{2}mv^2$$

Rotational:

$$K_{rot} = \frac{1}{2}I\omega^2$$

Work done

Work-energy theorem:

$$W = \Delta E = \Delta K + \Delta U$$

Constant force:

$$W = \vec F \cdot \vec s = |F||s|\cos\theta$$

Varying force:

$$W = \int \vec F \cdot d \vec x$$

Torque:

$$W = \int \tau d\theta$$

Power

$$P = \frac{dW}{dt}$$

Translational:

$$P = \vec F \cdot \vec v$$

Rotational:

$$P = \tau\omega$$

Motion on a circular path

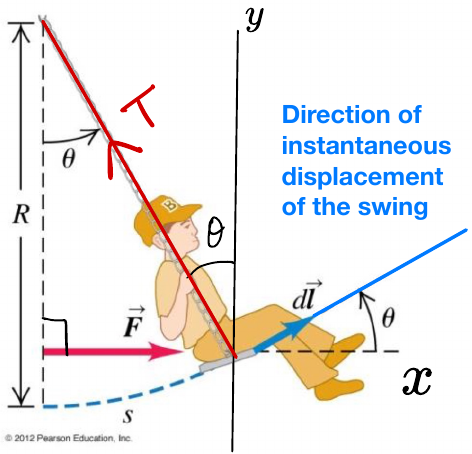
Example: person on a swing

$$\begin{align*} W_T &= 0 \\ W_F &= \int_0^\theta F\cos\theta dl = mgr(1-\cos\theta) \\ W_W &= \int_0^\theta mg\cos(\frac{\pi}{2}+\theta) dl = -mgr(1-\cos\theta) \\ W_{net} &= W_T + W_F + W_W = 0 \end{align*}$$

• $W_T$: work done by tension
• $W_F$: work done by external push
• $W_w$: work done by weight
• $r$: radius of the curved path
• $l$: displacement of the person